Multiscale#
Overview#
The multiscale module in SplineOps models signals and images as a hierarchy of spline approximations at progressively coarser resolutions. On top of this model, it provides reduction (spline filtering + dyadic decimation) and expansion (upsampling + spline interpolation), which are the building blocks of pyramid and wavelet transforms [1], [2], [3], [4].
Spline Representation#
A 1D discrete signal \(\{f[k]\}\) can be modeled as the continuous function
where \(\phi(x)\) is a polynomial spline basis function (e.g., a B-spline of degree 3), and \(c[k]\) are the spline coefficients determined from the samples \(f[k]\). This representation allows the application of downsampling and upsampling filters directly to the spline model.
Pyramid Decomposition#
Two key operators are proposed:
Reduce: it filters the signal (or image) and downsamples by dyadic factors, thus producing a coarse approximation.
Expand: it upsamples and interpolates the coarse approximation back to the original resolution.
When applied iteratively, these operations create a pyramid structure (approximation at multiple scales). In 2D, the same concept applies along rows and columns.
Subpixel Registration#
Method [5] does subpixel registration as least-squares matching of image intensities under a global transform (affine, optionally restricted to rigid/similarity) with an optional contrast change, and solves it with a modified Levenberg-Marquardt optimizer.
Its key ingredient is a spline pyramid: starting from a dyadic, least-squares fine-to-coarse decomposition built with cubic-spline filtering, the optimizer estimates the transform at the coarsest level and propagates the parameters down the pyramid so that finer levels only apply small corrections. The spline model (cubic) is used consistently for resampling and for computing exact spatial derivatives, which further stabilizes the coarse-to-fine.
A compact Python implementation following this approach is available in the GitHub repository glichtner/pystackreg.
Wavelet Decomposition#
We construct a spline-based multiscale basis (wavelets) by capturing the detail lost at each reduction step. The wavelet (detail) coefficients together with the final coarse approximation allow perfect reconstruction (synthesis).
The next figure, from Wavelet Decomposition, shows a three-level 2D Haar decomposition: the coarse approximation in the top-left corner and the horizontal, vertical, and diagonal detail sub-bands at each scale.
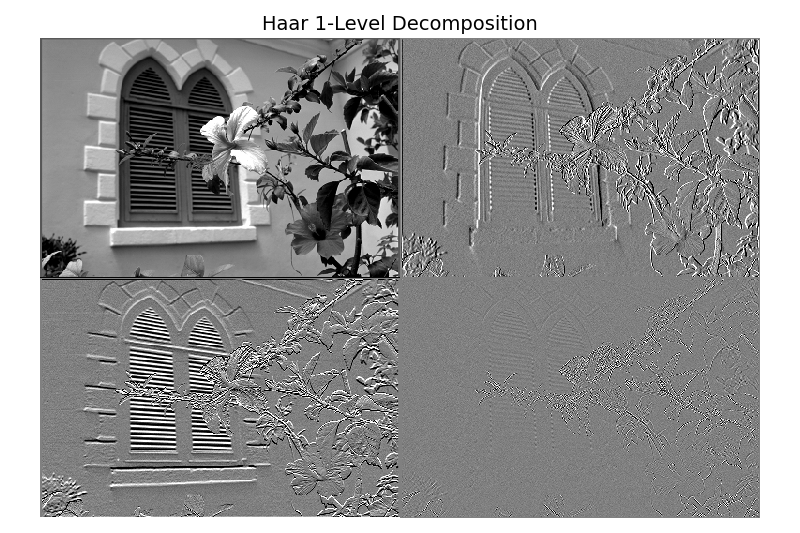
At each scale (analysis):
an approximation is obtained (the reduced signal or image);
a corresponding detail or wavelet sub-band is formed (the difference or “error” relative to the expanded approximation).
The application of this decomposition over multiple scales yields a so-called wavelet representation, where the stored approximation plus the detail coefficients can be used to perfectly reconstruct the original data (synthesis).
Implementation Details#
Reduce and expand features perform the core downsampling and upsampling based on spline filters.
Wavelet transforms such as Haar wavelets or spline wavelets (analysis and synthesis) are implemented by the combination of pyramid steps with detail sub-bands.
Various spline degrees (e.g., degree 3) are supported. They allow one to control how the data are dispatched in the approximation channel and the sub-bands.
