Standard Interpolation

Interpolate 2D images with standard interpolation. Compare them to SciPy zoom. We compute SNR and MSE on a face ROI (not the whole frame) to focus on detail and avoid boundary artifacts.

Imports

import numpy as np
import time

from urllib.request import urlopen
from PIL import Image
from scipy.ndimage import zoom as _scipy_zoom

from splineops.resize import resize
from splineops.utils.metrics import compute_snr_and_mse_region
from splineops.utils.plotting import plot_difference_image, show_roi_zoom
from splineops.utils.diagram import draw_standard_vs_scipy_pipeline


def fmt_ms(seconds: float) -> str:
    """Format seconds as a short 'X.X ms' string."""
    return f"{seconds * 1000.0:.1f} ms"


# You can switch this to np.float64 if you want full double precision.
DTYPE = np.float32

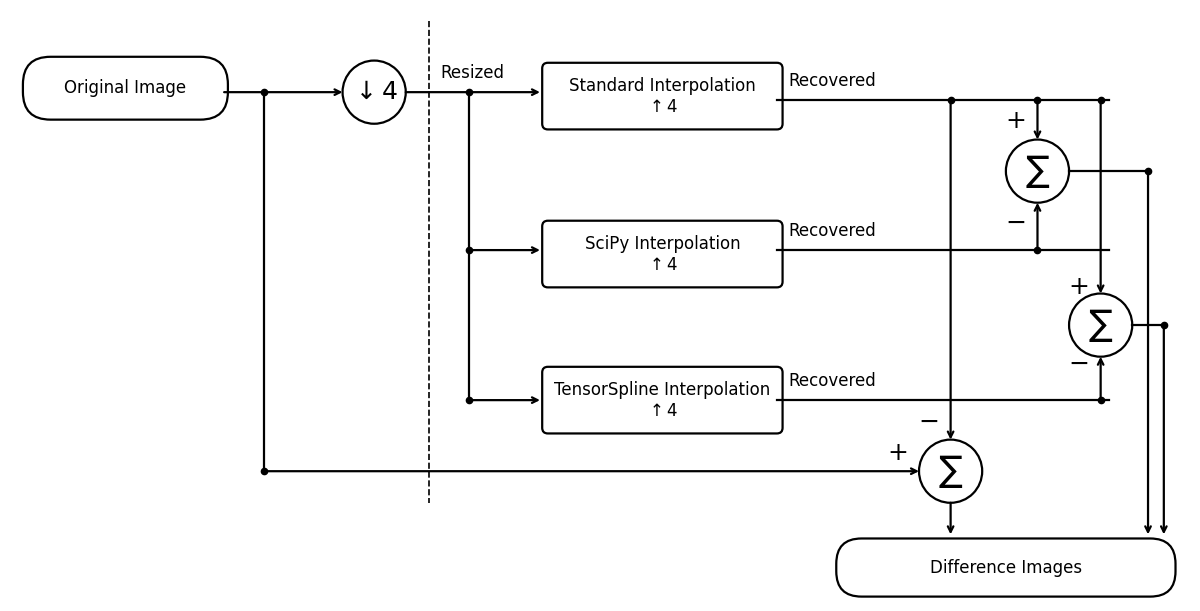
Pipeline Diagram

These experiments validate the standard interpolation against SciPy’s by showing they produce (nearly) the same result, and where tiny differences are.

_ = draw_standard_vs_scipy_pipeline(
    show_separator=True,          # keep dashed divider
    show_plus=False,              # no far-right '+'
    include_upsample_labels=True, # show '↑ 4' inside the boxes
    width=12.0                    # figure width in inches (height auto)
)

Load and Normalize an Image

Here, we load an example image from an online repository and convert to grayscale in [0, 1].

url = 'https://r0k.us/graphics/kodak/kodak/kodim14.png'
with urlopen(url, timeout=10) as resp:
    img = Image.open(resp)

# Start in float64 for robust normalization, then cast once to DTYPE.
data = np.array(img, dtype=np.float64)

# Convert to [0..1]
input_image_normalized = data / 255.0

# Convert to grayscale via simple weighting
input_image_normalized = (
    input_image_normalized[:, :, 0] * 0.2989 +  # Red channel
    input_image_normalized[:, :, 1] * 0.5870 +  # Green channel
    input_image_normalized[:, :, 2] * 0.1140    # Blue channel
)

# Run the interpolation backends in DTYPE (e.g. float32 for speed).
input_image_normalized = input_image_normalized.astype(DTYPE, copy=False)

zoom = np.pi / 6            # ≈ 0.5235987756
zoom_factors_2d = (zoom, zoom)
border_fraction = 0.3  # still available as a fallback (unused when roi=... is set)

# Face-centered 64×64 ROI (focus region for metrics & diffs)
ROI_SIZE_PX = 64
FACE_ROW, FACE_COL = 400, 600  # (row, col) approx center of the detail

h_img, w_img = input_image_normalized.shape

# Top-left of the 64×64 box, clipped to stay inside the image
row_top = int(np.clip(FACE_ROW - ROI_SIZE_PX // 2, 0, h_img - ROI_SIZE_PX))
col_left = int(np.clip(FACE_COL - ROI_SIZE_PX // 2, 0, w_img - ROI_SIZE_PX))

# ROI rectangle for metrics/plots (row, col, height, width)
roi_rect = (row_top, col_left, ROI_SIZE_PX, ROI_SIZE_PX)

roi_kwargs = dict(
    roi_height_frac=ROI_SIZE_PX / h_img,  # keeps height at 64 px (square ROI)
    grayscale=True,
    roi_xy=(row_top, col_left),           # top-left of the ROI
)

# Original (shifted ROI)
_ = show_roi_zoom(
    input_image_normalized,
    ax_titles=("Original Image", None),
    **roi_kwargs
)

Standard Interpolation

We use our standard interpolation method (cubic). SNR/MSE are computed on the face ROI.

# Forward + backward resize with splineops.resize.resize
t0 = time.perf_counter()
resized_2d_interp = resize(
    input_image_normalized,
    zoom_factors=zoom_factors_2d,
    method="cubic",
)
t1 = time.perf_counter()
recovered_2d_interp = resize(
    resized_2d_interp,
    output_size=input_image_normalized.shape,
    method="cubic",
)
t2 = time.perf_counter()

time_2d_interp_fwd = t1 - t0
time_2d_interp_back = t2 - t1
time_2d_interp = t2 - t0  # total pipeline time

# Metrics (ROI-aware)
snr_2d_interp, mse_2d_interp = compute_snr_and_mse_region(
    input_image_normalized,
    recovered_2d_interp,
    roi=roi_rect,
    border_fraction=border_fraction,
)

Resized Image

Show the resized image pasted on a white canvas (for zoom-out), plus the ROI zoom.

# Zoomed face detail for the resized (cubic) image pasted onto original-size canvas
h_res, w_res = resized_2d_interp.shape
zoom_r, zoom_c = zoom_factors_2d

# ROI size in the resized image (e.g., 64 -> 16 px when zoom=0.25)
roi_h_res = max(1, int(round(ROI_SIZE_PX * zoom_r)))
roi_w_res = max(1, int(round(ROI_SIZE_PX * zoom_c)))

# ROI center mapped into the resized image
center_r_res = int(round(FACE_ROW * zoom_r))
center_c_res = int(round(FACE_COL * zoom_c))

# Top-left of the ROI in the resized image, clipped to bounds
row_top_res = int(np.clip(center_r_res - roi_h_res // 2, 0, h_res - roi_h_res))
col_left_res = int(np.clip(center_c_res - roi_w_res // 2, 0, w_res - roi_w_res))

# --- Build original-size white canvas and paste the small resized image at top-left (0,0) ---
canvas = np.ones((h_img, w_img), dtype=resized_2d_interp.dtype)  # white background in [0,1]
canvas[:h_res, :w_res] = resized_2d_interp

roi_kwargs_on_canvas = dict(
    roi_height_frac=roi_h_res / h_img,   # keeps the inset square at roi_h_res pixels high
    grayscale=True,
    roi_xy=(row_top_res, col_left_res),  # same coords since pasted at (0,0)
)

_ = show_roi_zoom(
    canvas,
    ax_titles=(f"Resized Image (standard, {fmt_ms(time_2d_interp_fwd)})", None),
    **roi_kwargs_on_canvas
)

Recovered Image (Standard)

We plot the recovered image (after reversing the zoom) with the same ROI.

_ = show_roi_zoom(
    recovered_2d_interp,
    ax_titles=(f"Recovered Image (standard, {fmt_ms(time_2d_interp_back)})", None),
    **roi_kwargs
)

SciPy Interpolation

For comparison, we also use SciPy’s zoom method. Metrics are computed on the ROI. SciPy preserves the input dtype, so it will also run in DTYPE here.

t0 = time.perf_counter()
resized_2d_scipy = _scipy_zoom(
    input_image_normalized,
    zoom_factors_2d,
    order=3,
)
t1 = time.perf_counter()
recovered_2d_scipy = _scipy_zoom(
    resized_2d_scipy,
    1.0 / np.asarray(zoom_factors_2d),
    order=3,
)
t2 = time.perf_counter()

time_2d_scipy_fwd = t1 - t0
time_2d_scipy_back = t2 - t1
time_2d_scipy = t2 - t0  # total pipeline time

snr_2d_scipy, mse_2d_scipy = compute_snr_and_mse_region(
    input_image_normalized,
    recovered_2d_scipy,
    roi=roi_rect,
    border_fraction=border_fraction,
)

Recovered Image (SciPy)

_ = show_roi_zoom(
    recovered_2d_scipy,
    ax_titles=(f"Recovered Image (SciPy, {fmt_ms(time_2d_scipy_back)})", None),
    **roi_kwargs
)

Difference Images

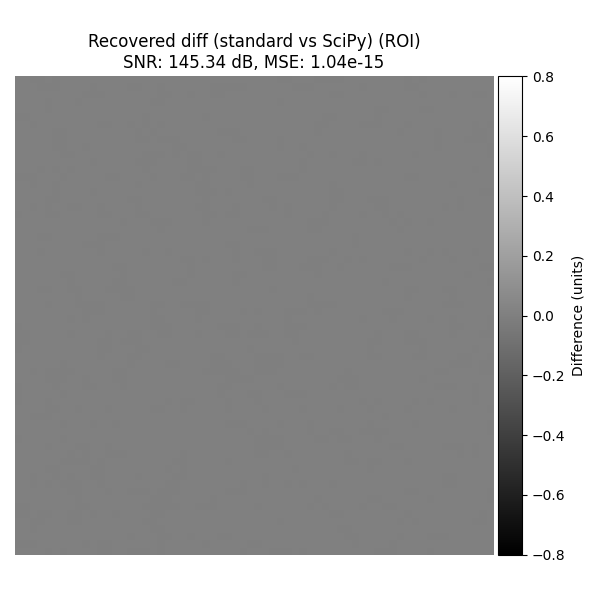
Standard vs SciPy

Compare the two recovered images on the face ROI and plot that difference.

snr_scipy_vs_interp, mse_scipy_vs_interp = compute_snr_and_mse_region(
    recovered_2d_scipy, recovered_2d_interp, roi=roi_rect
)

plot_difference_image(
    original=recovered_2d_scipy,
    recovered=recovered_2d_interp,
    snr=snr_scipy_vs_interp,
    mse=mse_scipy_vs_interp,
    roi=roi_rect,
    title_prefix="Recovered diff (standard vs SciPy)",
)

Original vs Standard

For completeness, show the difference image (original - recovered with standard interpolation) on the ROI.

plot_difference_image(
    original=input_image_normalized,
    recovered=recovered_2d_interp,
    snr=snr_2d_interp,
    mse=mse_2d_interp,
    roi=roi_rect,
    title_prefix="Difference (original vs standard)",
)

Alternative using TensorSpline

As an alternative, we can replicate the same interpolation manually using the TensorSpline class, which underpins the resize() function behind the scenes.

from splineops.spline_interpolation.tensor_spline import TensorSpline

# 1) Build uniform coordinate arrays that match the shape of 'input_image_normalized'
height, width = input_image_normalized.shape

# Use the same dtype as the image for coordinates, so everything lives in DTYPE.
x_coords = np.linspace(0, height - 1, height, dtype=input_image_normalized.dtype)
y_coords = np.linspace(0, width - 1, width, dtype=input_image_normalized.dtype)
coordinates_2d = (x_coords, y_coords)

# 2) For "cubic interpolation", pick "bspline3".
#    For boundary handling, we can pick "mirror", "zero", etc.
ts = TensorSpline(
    data=input_image_normalized,
    coordinates=coordinates_2d,
    bases="bspline3",  # cubic B-splines
    modes="mirror"     # handles boundaries with mirroring
)

# 3) Define new coordinate grids for the "zoomed" shape.
zoomed_height = int(height * zoom_factors_2d[0])
zoomed_width  = int(width  * zoom_factors_2d[1])

x_coords_zoomed = np.linspace(
    0, height - 1, zoomed_height, dtype=input_image_normalized.dtype
)
y_coords_zoomed = np.linspace(
    0, width  - 1, zoomed_width,  dtype=input_image_normalized.dtype
)
coords_zoomed_2d = (x_coords_zoomed, y_coords_zoomed)

# Evaluate (forward pass): zoom in or out
resized_direct_ts = ts(coordinates=coords_zoomed_2d)

# 4) Define coordinate grids for returning to the original shape
x_coords_orig = np.linspace(
    0, height - 1, height, dtype=input_image_normalized.dtype
)
y_coords_orig = np.linspace(
    0, width  - 1, width,  dtype=input_image_normalized.dtype
)
coords_orig_2d = (x_coords_orig, y_coords_orig)

# Evaluate (backward pass): from zoomed shape back to original
ts_zoomed = TensorSpline(
    data=resized_direct_ts,
    coordinates=coords_zoomed_2d,
    bases="bspline3",
    modes="mirror"
)
recovered_direct_ts = ts_zoomed(coordinates=coords_orig_2d)

# Now, resized_direct_ts / recovered_direct_ts should be very similar
# to 'resized_2d_interp' / 'recovered_2d_interp' from the high-level "resize()" approach.
# Let's compute MSE to confirm:
mse_forward  = np.mean((resized_direct_ts  - resized_2d_interp ) ** 2)
mse_backward = np.mean((recovered_direct_ts - recovered_2d_interp) ** 2)
print(f"MSE (TensorSpline vs. resize()) resized:  {mse_forward:.6e}")
print(f"MSE (TensorSpline vs. resize()) recovered: {mse_backward:.6e}")

MSE (TensorSpline vs. resize()) resized:  7.308340e-13
MSE (TensorSpline vs. resize()) recovered: 1.133354e-12