Extension modes

Plotting different extension modes of signals.

Imports and Utilities

Visualize how the extension modes allow one to control the values that a signal is assumed to take outside of its original domain. Generate a signal that is mostly linear but includes a “bump.”

import numpy as np
import matplotlib.pyplot as plt
from splineops.interpolate.tensorspline import TensorSpline

x_values = np.linspace(0, 6, 101)

def create_signal_with_bump(x_values, bump_location=3, bump_width=0.5, bump_height=5):
    linear_part = x_values
    bump = np.where(
        (x_values > (bump_location - bump_width / 2))
        & (x_values < (bump_location + bump_width / 2)),
        bump_height,
        0,
    )
    return linear_part + bump

def plot_extension_modes_for_bump_function(mode_name, x_values, title):
    plt.figure(figsize=(12, 6))
    data = create_signal_with_bump(x_values)
    tensor_spline = TensorSpline(
        data=data, coordinates=(x_values,), bases="linear", modes=mode_name
    )
    eval_x_values = np.linspace(-10, 10, 2000)
    extended_data = tensor_spline.eval(coordinates=(eval_x_values,))
    plt.plot(eval_x_values, extended_data, label="Extended Signal")
    plt.axvline(x=x_values[0], color="red", linestyle="--", label="Original Start")
    plt.axvline(x=x_values[-1], color="blue", linestyle="--", label="Original End")
    plt.title(title)
    plt.xlabel("x")
    plt.ylabel("Interpolated Value")
    plt.grid(True)
    plt.legend()
    plt.show()

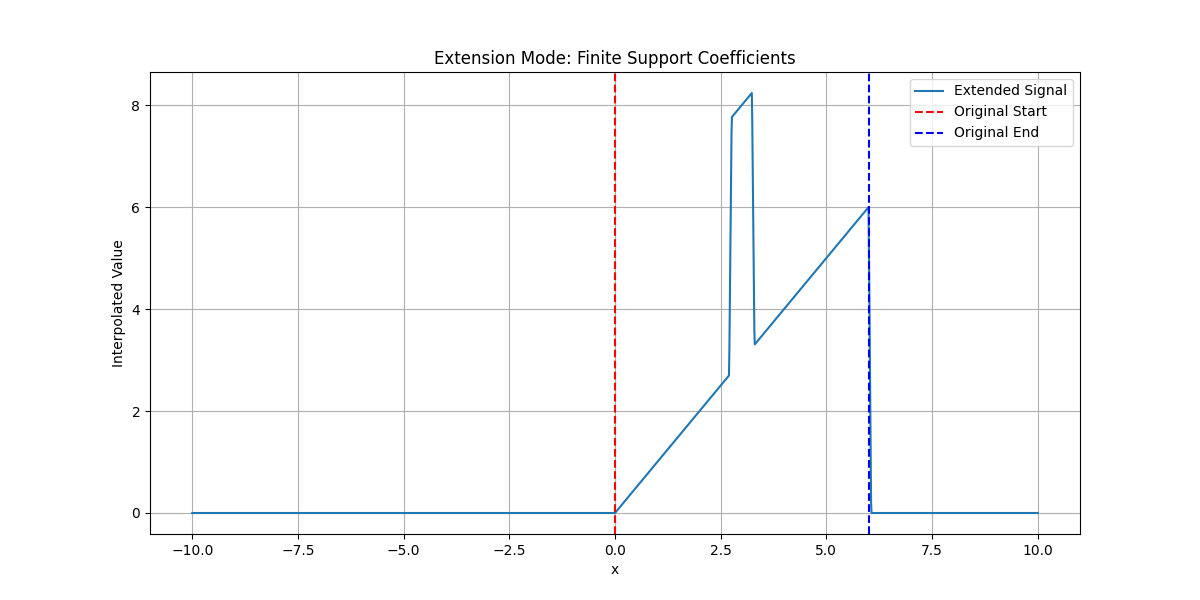
Finite-Support Coefficients

plot_extension_modes_for_bump_function(
    mode_name="zero",
    x_values=x_values,
    title="Extension Mode: Finite Support Coefficients",
)

Narrow Mirroring

plot_extension_modes_for_bump_function(
    mode_name="mirror",
    x_values=x_values,
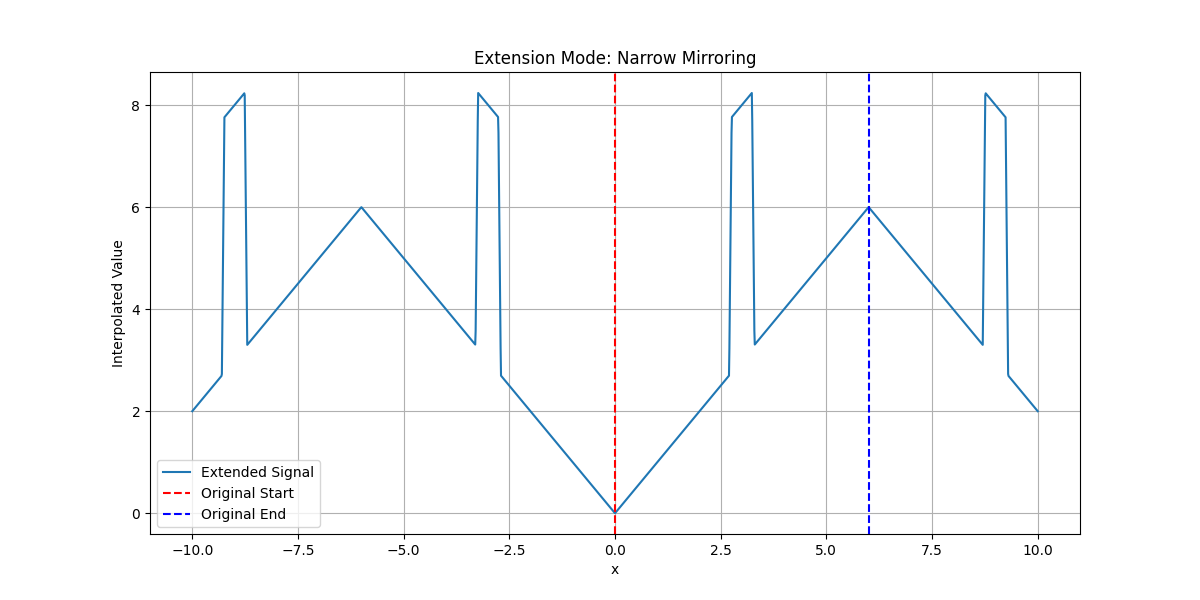
    title="Extension Mode: Narrow Mirroring",
)

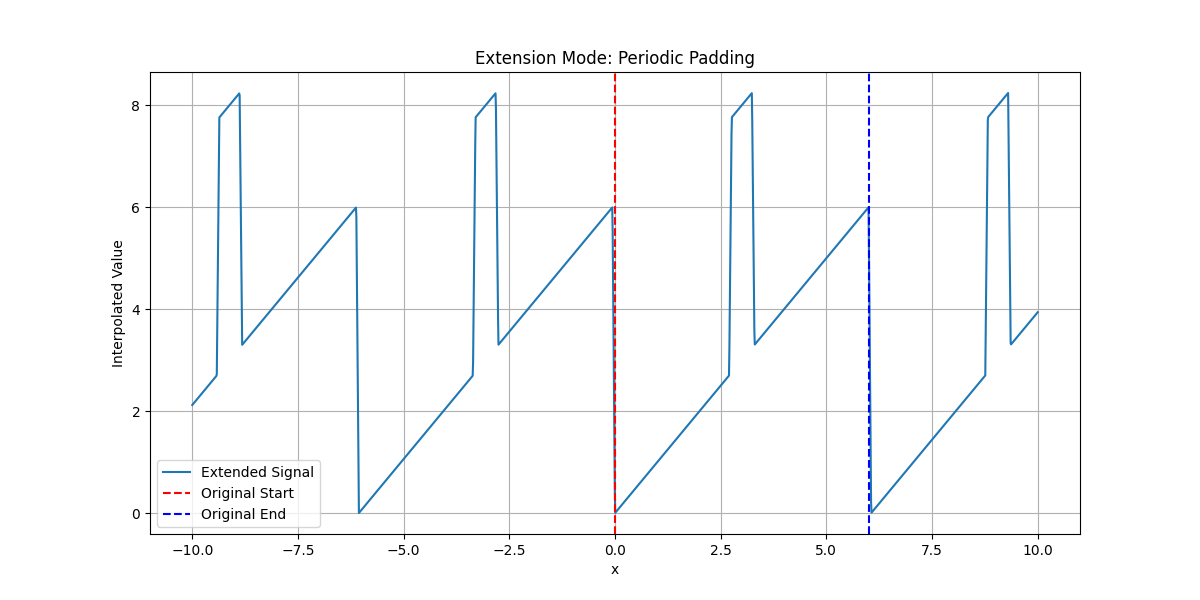
Periodic Padding

plot_extension_modes_for_bump_function(
    mode_name="periodic",
    x_values=x_values,
    title="Extension Mode: Periodic Padding",
)