Recursive Smoothing Spline

We plot a recursive smoothing spline with different parameters.

Imports

import math
import numpy as np
import matplotlib.pyplot as plt
from splineops.denoise.smoothing_spline import smoothing_spline
from splineops.denoise.smoothing_spline import recursive_smoothing_spline

Recursive Smoothing Spline

# Example signal: A noisy sine wave
x = np.linspace(0, np.pi, 100)
signal = np.sin(x) + 0.1 * np.random.normal(size=x.shape)

# Different values for the smoothing parameter in recursive smoothing spline
lam_values = [0.005, 0.05, 0.1]  # You can try smaller or larger values

# Apply fractional smoothing spline as a baseline for comparison
lambda_ = 0.1  # Regularization parameter for fractional method
m = 1          # No upsampling
gamma = 0.6    # Spline order parameter
_, smoothed_fractional = smoothing_spline(signal, lambda_, m, gamma)

# Compute MSE values for different recursive smoothing spline parameters
mse_values = []

# Plot results
plt.figure(figsize=(12, 8))
plt.plot(x, signal, label="Noisy Signal", linestyle="--", color="gray")
plt.plot(x, smoothed_fractional, label="Fractional Smoothing Spline", color="red")

# Apply and plot recursive smoothing spline for each lambda value
for lam_recursive in lam_values:
    smoothed_recursive = recursive_smoothing_spline(signal, lamb=lam_recursive)

    # Compute MSE
    mse = np.mean((smoothed_recursive - smoothed_fractional) ** 2)
    mse_values.append(mse)

    plt.plot(x, smoothed_recursive, label=f"Recursive Smoothing (λ={lam_recursive})")

# Print MSE values
print("\nMean Squared Error (MSE) between Recursive and Fractional Smoothing Spline:")
for lam, mse in zip(lam_values, mse_values):
    print(f"λ={lam:.3f}: MSE = {mse:.6f}")

plt.legend()
plt.xlabel("x")
plt.ylabel("Signal Value")
plt.title("Comparison of Recursive Smoothing with Different λ Values")
plt.show()

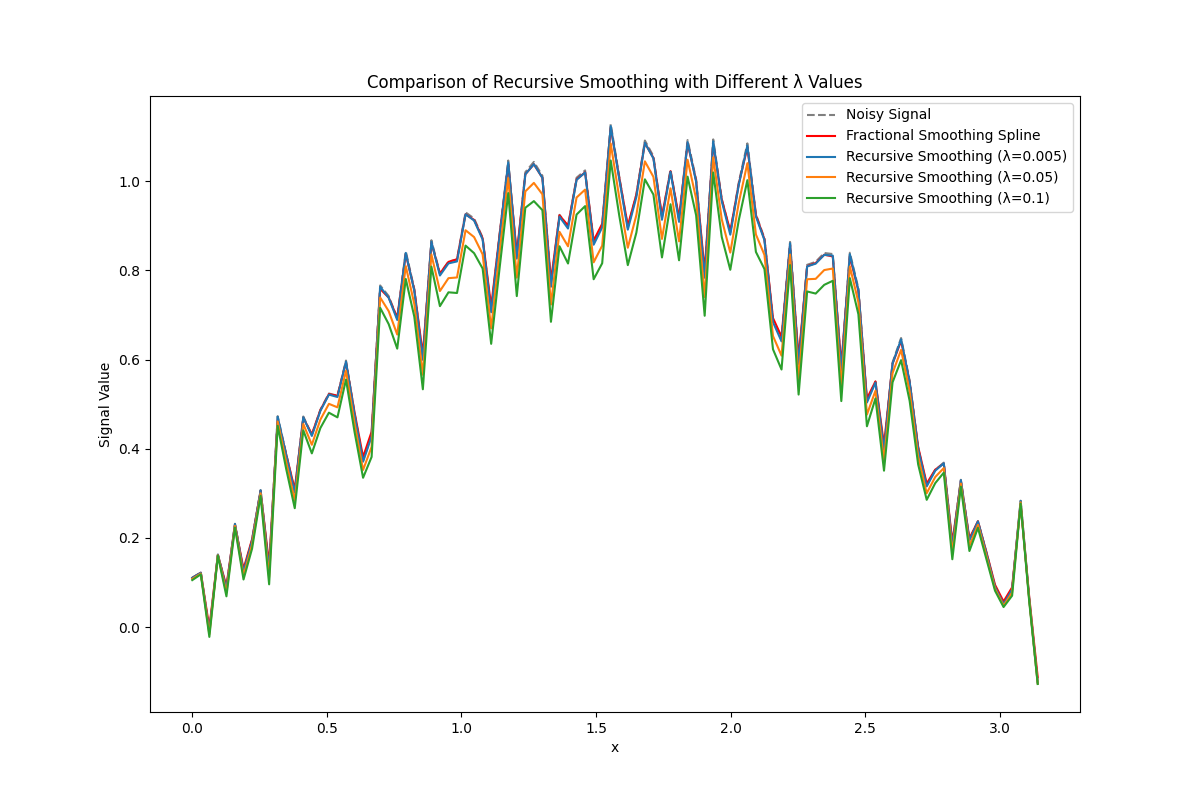
Mean Squared Error (MSE) between Recursive and Fractional Smoothing Spline:
λ=0.005: MSE = 0.000035
λ=0.050: MSE = 0.001070
λ=0.100: MSE = 0.003683